Enjoyable Physics Experiments
$$\int \int \int $$
Try this out
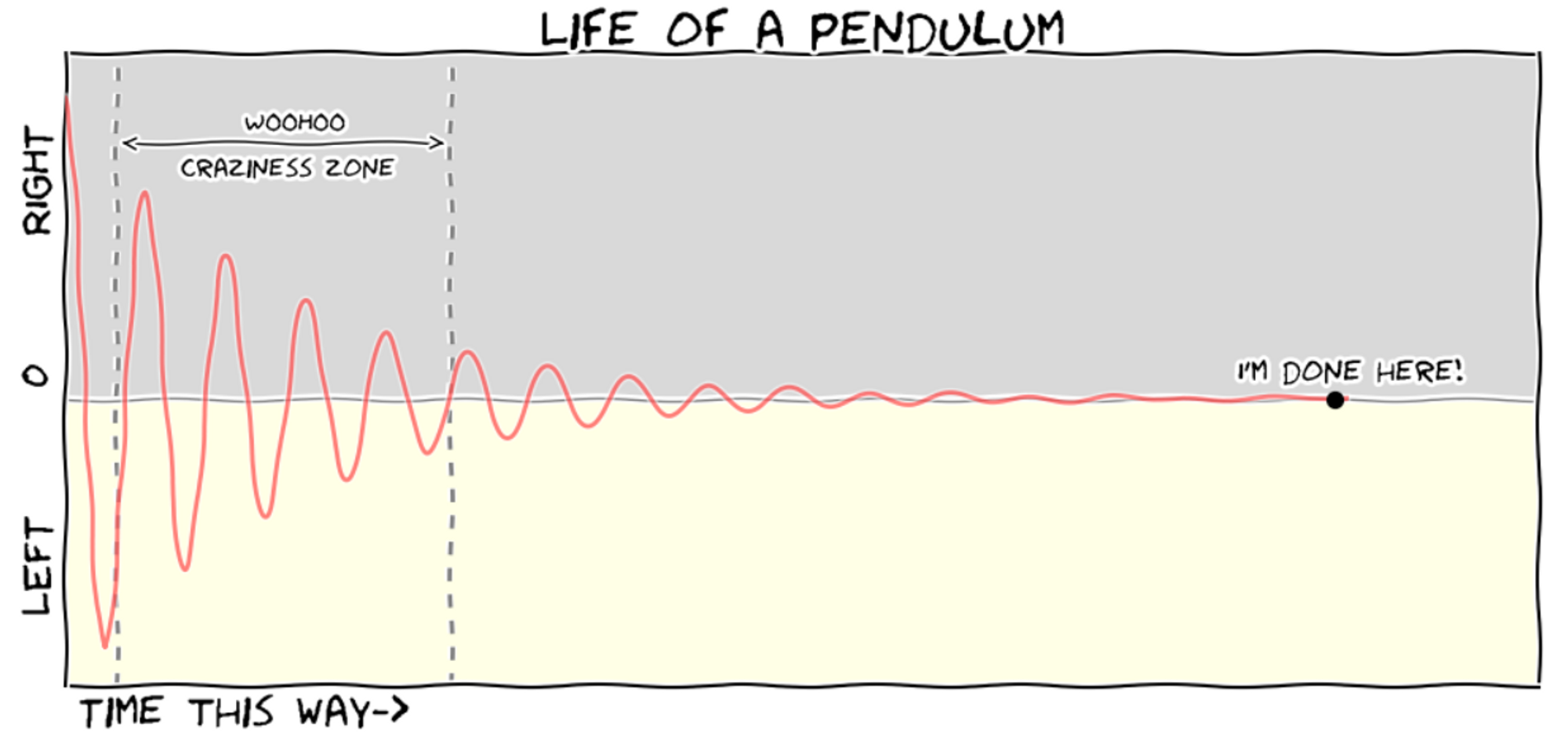
Balance your smartphone on your finger and start the measurement. It should oscillate like shown below.

.
If it does not work:
1. copy/paste this in a new tab to enable sensors:
chrome://flags/#enable-generic-sensor-extra-classes
How do we explain the graph above?
Most oscillations die out. That is because there are dissipating forces acting on the object that is oscillating. It is loosing energy by producing either sound, electromagnetic waves or temperature.
What is an example of a decaying oscillation that we all are familiar with?
Listen to the sound below and observe the intensity plot. What do you notice?
A physics approach to the decaying oscillation
For an object that is oscillating, the Amplitude (how much it’s moving) is described by
$$A(t) = e^{-t/\tau} \sin(\omega t)$$
The $e^{-t/\tau}$ is describing the decay of the oscillation. Use the app below to look at the shape of $e^{-t/\tau}$. How does it depend on $\tau$?
How to use the graphing app?
Edit the formula below.
